地統計學是對統計的研究,重點是時空信息。目的是建模和發現地理現象的模式。
地統計學領域涵蓋了廣泛的空間統計主題,例如:
- 半變異函數表征數據中的空間格局
- 克里格法用于空間預測
- 測量未采樣值不確定性的標準誤差
地統計學是一個不斷發展的研究領域,用于采礦,氣候研究,土壤科學和大多數環境領域。
為什么要使用地統計學?
地統計學提供的三個主要工具是:

添加微信好友, 獲取更多信息
復制微信號
- 半變異函數用于模擬所有成對點之間的關系。
- 克立格模型用于預測未采樣位置的值。
- 在未采樣值下測量置信度的標準誤差。
例如,如果在特定位置有土壤樣品,則地統計學可以回答以下類型的問題:
未采樣地點的土壤水分的預測量是多少?
對土壤水分含量的空間預測的真實性有多可靠?
這與確定性插值技術(例如反距離權重(IDW))不同,后者僅估算未知位置。
通常,IDW使用預定義的冪函數。然后結果就是這樣。但這并不能說明您有多自信。
閱讀更多:克里格插值法–在這一方面的預測很強。
地統計學工具和主題
半變異函數
地統計學提供了諸如半變異函數之類的描述性工具來識別空間現象的潛在趨勢。根據托伯勒的《地理之一定律》,距離較近的事物比距離較遠的事物更相關。這也是空間自相關概念的主要思想。
半變異函數根據距離繪制出所有數據對。 較近的觀測值具有較高的相關性。但是,在一定距離(范圍)內,彼此靠近的點之間不再存在關系。
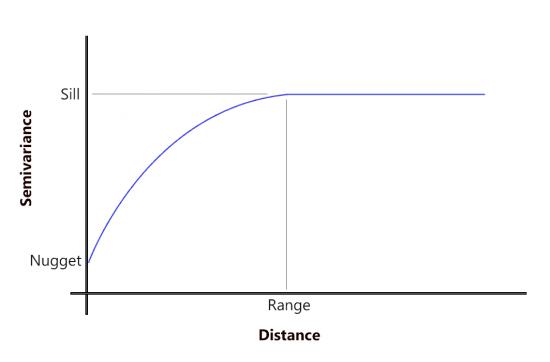
半變異函數描述了這種關系,直到它到達不再與其他樣本相關為止,目的是擬合一個數學函數,該函數可以對半變異函數中的趨勢進行建模。
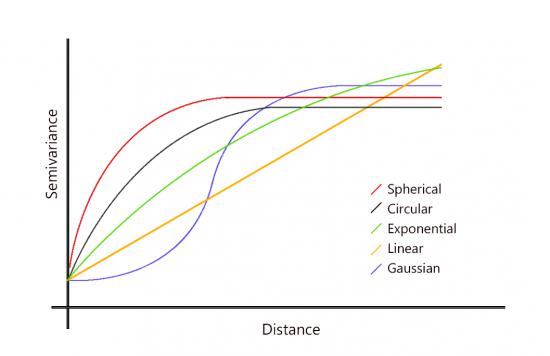
例如,可以選擇一個半變異函數:
- 球形
- 高斯
- 圓形
- 線性
- 指數
克里金插值
克里金(Kriging)是一種插值技術,利用樣本之間的空間相關性來預測未采樣位置的值。主要區別在于可使用從半變異函數獲得的數學函數來構建。
以下是地統計中可用的不同克里金法類型:
協同克里金添加了第二個相關變量,可使用輔助信息來改善預測。例如,要預測山區的降雨量變化,可以將海拔數據作為降雨量的協變量添加。
經驗貝葉斯克里金法(EBK)可以通過分別處理局部方差來提供幫助。EBK并非在整個范圍內都具有相似的方差,而是在不同區域中將克里金法作為單獨的基礎過程進行,仍然執行克里金法,但在本地完成。
通用克里金法通過考慮趨勢來與普通克里金法一起添加趨勢面分析(或漂移)。
指標克里金法使用諸如城市和非城市小區之類的二進制數據(0和1)進行普通克里金法。
概率克里金法使用二進制數據(類似于指標克里金法)并估計一系列截止點的未知點。
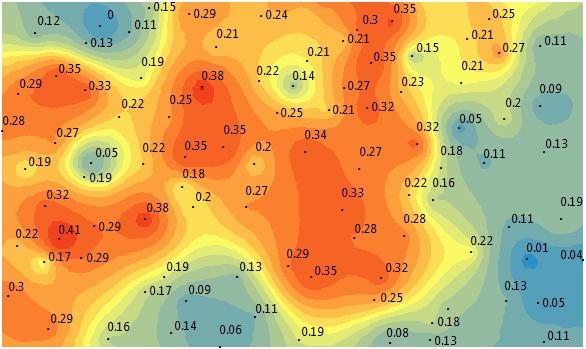
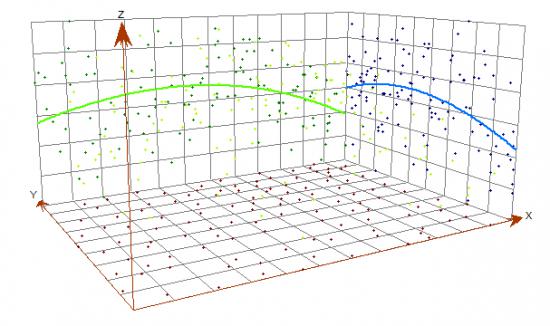
此示例顯示了來自克里金法的空間預測模型。
標準誤差
地統計學的優勢在于,它可以使用標準誤差表面圖來評估未采樣值的不確定性。標準錯誤圖表示對預測可能性為真的置信度的度量。
標準誤差評估了克里金模型的穩健性。通過比較實際值和預測值,構建殘差表面來評估不確定性。
通常,當觀測值稀疏時,會得到更高的錯誤標準。當誤差超過臨界閾值時,專業知識可有助于變異函數的處理。
應用與用途
地統計學最初是為采礦業開發的,用于估計和管理礦石和礦產資源。
但是,地統計學適用于具有局部變化的各種類型的空間現象。例如,用于:
- 預測天氣,氣候,污染和其他大氣現象。
- 評估各種規模的土壤屬性和化學性質。
- 衡量漁業中可持續種群的魚類豐度。
- 地統計學是工程,地球物理學和大多數自然現象的新興研究領域。
來源:開源地理空間基金會中文分會
來源鏈接:https://www.osgeo.cn/post/1f612
本站聲明:網站內容來源于 *** ,如有侵權,請聯系我們,我們將及時處理。








