為針對傳統曲線特征點的提取 *** 均采用Douglas-Peucher(D-P)算法給定閾值的思路，在曲度較大處易造成一 些重要特征點缺失，在彎曲的水平距離較小處易造成非特征點保留的問題，該文提出一種改進的曲線特征點提取 *** ，通過自適應來提取曲線的全局特征點，即通過標準差分別計算出間隔點連線的參考值和中間點到該線垂線的參考值，比較曲線上每個點的彎曲程度與曲線整體彎曲程度的大小，來提取曲線的全局特征點。以道路和河流的實際線數據進行了實驗，結果表明，該 *** 不僅很好地保持了曲線整體形狀特征，而且大幅降低了壓縮誤差、提高了精度。

關鍵詞：特征點；統計法；自適應；標準差；彎曲度

微信號：MeetyXiao
添加微信好友, 獲取更多信息
復制微信號

能夠概括曲線基本形狀的點叫做曲線的特征點[1]。線要素化簡算法[2-5]的核心思想是在盡可能保持曲線形狀特征的前提下，減少其節點的數量， 所以準確提取特征點十分重要。目前單線壓縮的算法已經較為成熟，曲線特征點的提取主要基于垂距、斜率、角度等[6-10] *** ，垂距法具有旋轉不變性和位移不變性的優點，受到廣泛的應用。垂距法來源于經典D-P算法，通過預先給定閾值，再比較曲線上的點到曲線首末端點連線 的垂距與給定閾值的大小，來提取特征點；很多算法都是在此基礎上進行了改進，如：文獻[11]提出的面向自然岸線抽稀的改進D-P算法，該算法是將曲線上的一些特殊凸點作為分段點，使用D-P進行化簡，提取自然岸線凸點作為備選分段點集，根據凸點與相鄰兩點組成的三角形面積大小篩選分段點，接著利用相鄰分段點作為D-P算法的首尾點，以基于最小二乘法的擬合曲線選定更優距離閾值，并作為初始閾值，進行逐段抽稀。文獻 [12]提出的基于Ping的D-P算法抽稀閾值優化選取，將測深條帶中每Ping數 據看做一條空間曲線，然后利用D-P算法進行多波束測深數據的抽稀，選取不同抽稀閾值對Ping進行抽稀運算；文獻[13]提出的矢量數據壓縮算法的實現與改進，即徑向約束D-P算法，通過預先給定的垂距閾值和徑向約束閾值，然后比較曲線上的點到曲 線首末端點連線的垂距與給定閾值的大小，再比較曲線上的點到曲線首末端點連線的值與給定徑向約束閾值 的大小，來提取特征點；上述算法基本上都是D-P算法的延伸和拓展，通 過給定閾值的方式來提取特征點，在曲度較大處易造成一些重要特征點缺失，在彎曲的水平距離較小處易造成一些非特征點的保留。本文針對徑向約束D-P算法[13]提取曲線全局特征點的不足，提出了一種全新的曲線全局特征點的識別 *** 。通過標準差分別計算出間隔點連線的參考值和中 間點到該線垂線的參考值，通過比較曲線上每個點的彎曲程度與曲線整體彎曲程度[14]的大小，來提取曲線的全局特征點。

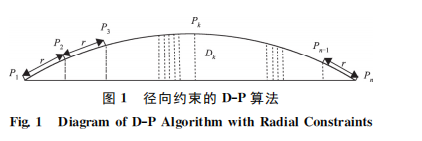
１）D-P算法。D-P算法是曲線矢簡量數據壓縮 的一種常用而有效的算法，利用遞歸過程能夠非常簡潔的完成算法實現，先連接曲線首尾兩點構成一條直線，然后計算曲線上其余各個點到該直線的距離ｄ，選取其中的更大值Dk與規定的臨界值Ｄ作比較，若曲線上的點到該直線上距離的更大值Dk都小于規定的臨界值Ｄ，則直接舍去曲線上首尾間的各個點，若曲線上的點到該直線上距離的更大值Dk不小于規定的臨界值Ｄ，則保留曲線上的該點。以圖１為例，具體步驟如下：①設曲線由點序P１，P２，…，Pｎ構成，取P１，Pｎ為首尾兩點；②計算曲線上所有內點Pｉ（ｉ＝２，３，…， ｎ－１）到直線P１Pｎ的距離Dｉ，選取曲線上的點到直線距離更大的點Pk；③判斷曲線到直線P１Pｎ上的更大距離Dk與給定的臨界值Ｄ的大小，若Dk小于給定的臨界值，則該點不是特征點，若Dk不小于給定的臨界值，則該點Ｐｋ成為特征點。

２）帶有徑向約束的D-P算法。D-P算法僅利用 垂向距離作為約束條件來決定曲線內點的取舍，當給定的臨界值差別比較大時，會導致曲線 的壓縮結果完全不同；該算法在大比例尺度壓縮過程中不能有效控制面積誤差[15]，致使壓縮后的面積與原圖形面積差距比較大；文獻[13]針對這些問題引進了徑向距離約束條件的 *** ，提出了一種矢 量數據壓縮的D-P算法的實現與改進，降低了壓縮后圖形面積與原圖形面積的誤差，取得了較好的效果。該算法的基本思想是在D-P算 法②、③ 中間加一個徑向約束條件ｒ，步驟如下：步驟的① 和②不變；③給定徑向約 束 條 件ｒ；ｒ為 曲線 一 定距離的弧段；④判斷曲線到直線P１Pｎ上的更大 距離Dk與給定的臨界值Ｄ的大小，若Dk小于給定臨界值，則再判斷｜PKP１｜或｜PKＰｎ｜的距離與徑向約束條件ｒ的大小，只要有一個距離大于徑向約束條件ｒ，則點PK仍作為特征點保留；若 Dk不小于給定的臨界值，則該點為特征點。

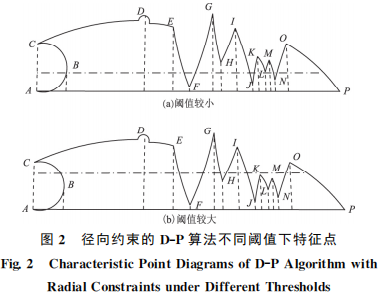
該壓縮算法仍然采用D-P 算法的思路，導致在曲線曲度較大處易 造成一些重要特征點缺失， 在彎曲的水平距離較小處易造成非特征點的保留，最終影響壓縮后的圖形效果[16]。見圖２（ａ），該閾值下特征點為B、C、Ｄ、Ｅ、Ｇ、Ｈ、Ｉ、Ｋ、Ｌ、 Ｍ、Ｏ。由于閾值較小，在彎曲的水平距離較小處 造成非特征點 Ｄ、Ｋ、Ｍ 的 保 留，見 圖２（ｂ），該閾值下特征點為Ｃ、Ｄ、Ｅ、Ｇ、Ｉ、Ｏ。由于閾值較大，在彎曲的水平距離較小處造成非特征點Ｄ的保留以及在曲度較大處造成特征點 Ｂ、Ｆ 的缺失。

本文針對大比例尺下徑向約束D-P算法提取曲 線全局特征點 *** 的不足，結合基于D-P算法特征點的選取 *** 與基于帶有徑向約束D-P算法特征點 的選取 *** ，提出一種改進的曲線特征點提取 *** 。核心內容為通過自適應來提取曲線的全局特征點， 先分別計算出點到間隔點連線垂距的平均數和中位數以及間隔點連線的平均數和中位數，再通過比較各自的標準差，選取各自更優的平均數或中位數作為能否保留曲線特征點的參考值，最后通過比較曲 線上每個點的彎曲程度與曲線整體彎曲程度[17-18]的 大小，來提取曲線的全局特征點。線要素化簡算法的核心思想是在盡可能保持 曲線形狀特征的前提下，減少其節點的數量，同時盡可能多地保留 曲線全局特征點。提取曲線全局特征點主要有以下４個步驟，見圖３。

１）遍歷曲線上所有的點，連接曲線上的每一個間隔點，同時過中間點做間隔點連線的垂線，見圖３，依次類推，直至遍歷完曲線上所有的點，垂線分別記為 Ｍ１、Ｍ２、Ｍ３…，間隔點連線的長度分別記為 Ｎ１、Ｎ２、Ｎ３…。

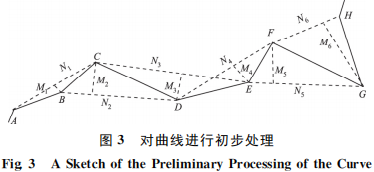
２）統計出每條垂線的長度 Ｍ 以及每一條間隔點 連線的長度Ｎ，計算出垂線的中位數 ＭＰ、平均數ＭＱ和標準差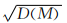，同時計算出間隔點連線長度的中位數ＮＰ、平均數ＮＱ和標準差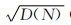（這里的 標準差是指分別以中位數為參考值求出的標準差和 以平均數為參考值求出的標準差），標準差反映一組 數據的離散程度，標準差越小離散程度越小，標準 差越大離散程度越大，見表１和式（１）～式（８）。

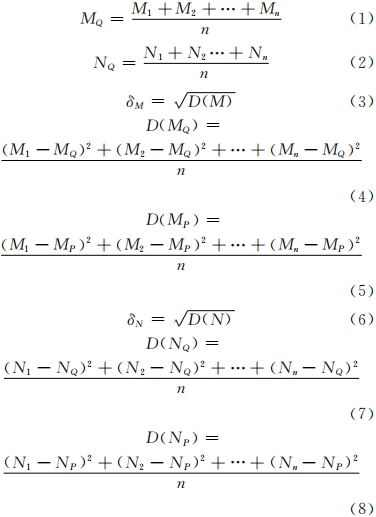
中位數：將一組數從大到小或從小到大進行有序排列，位于最中間的那個數稱為中位數。ＭＱ表示垂線的平均數，ＮＱ表示間隔點連線的平均數；ＭＰ表示垂線的中位數，ＮＰ表示間隔點連線的中位 數；δＭ表示垂線的標準差，δＮ 表示間隔點連線的標準差；D(M)表示垂線的方差，D(N)表示間隔點連線的方差。

３）分別比較以平均數為參考值求出的標準差和以中位數為參考值 求出的標準差值的大小，若以中位數ＭＰ為參考值計算出標準差的值小，則以垂線的中位數ＭＰ為參考值；若以平均數ＭＱ為參考值計算出的標準 差的值小，則以垂線的平均數ＭＱ為參考值。同理，若以中位數ＮＰ為參考值計算出的標準差的值小，則以間隔點連線的中位數ＮＰ為參考值；若以平均數ＮＱ為參考值計算出的標準差的值小，則以間隔點連線的平均數 ＮＱ為參考值。

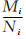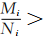
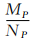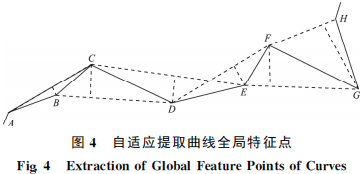
４）表示曲線在i點的彎曲程度，比值越大表示曲線在該點處的彎曲程度越大，比值越小表示曲線在該點處的彎曲程度越小。這里以各自 的中位數作為參考值來說明本文的 *** ：如果 ，那么表明曲線在該點處彎曲程度較大，則選取該點作為曲線的一個特 征點；如果 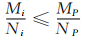 ，那么表明曲線在該點處彎曲程 度較小，則不選取該點作為曲線的特征點；依次類推直至遍歷完曲線上 所有的特征點，ＡＢＣＤＥＦＧＨ為原折線，ＡＣＤＥＦＧＨ為本文算法自適應后的折線見圖４。

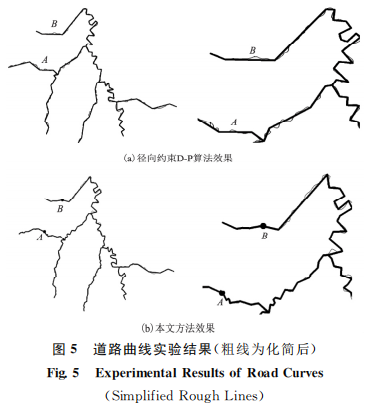
在相同的參數條件下用兩種算法分別對道路和河流數據進行化簡，圖５和圖６分別截取了部分化簡結果，在處理道路、河流等曲度較平緩、彎曲水平距離較大處的線群密集要素時，徑向約束D-P算法化簡效率較高，但是在曲度較大處、彎曲水平距離較小處時化簡結果顯得較粗糙，原因是由于垂距閾值和徑向約束閾值的隨機性，導致在曲度較大處一些重要特征點的丟失和彎曲水平距 離較小處一些非特征點的保留造成 的（圖５（ａ）Ａ、Ｂ 處及圖６（ａ）Ａ、Ｂ、Ｃ、Ｄ 處）。本文算法通過自 適應來提取曲線的全局特征點，化簡結果與原始數據貼合緊密，不僅精確地提取了曲度較大處的特征點，同時避免了彎曲水平距離較小處非特征 點的保留，保證了曲線原有的形狀特征不發生明 顯變化（圖５（ｂ）及圖６（ｂ））。對比道路、河流兩幅圖的化簡結果，當線要素曲度平緩而彎 曲水平距離較大時，改進的效果并不明顯，而對于曲度較大同時彎曲水平 距離較小的線要素區域，本文算法的化簡效果明顯優于徑向約束D-P算 法，在保證了 曲線壓縮的同時，以更大限度保留了曲線原來的形狀特征。

１）以道路曲線進行實驗效果圖對比。圖５為分 別依據徑向約束D-P算法和本文 *** 提取道路曲線全局特征點的結果。用D-P算法提取曲線全局特征點的局部效果見圖５（ａ）；用本文算法提取 曲 線全局特征點的局部效果，見圖５（ｂ）。

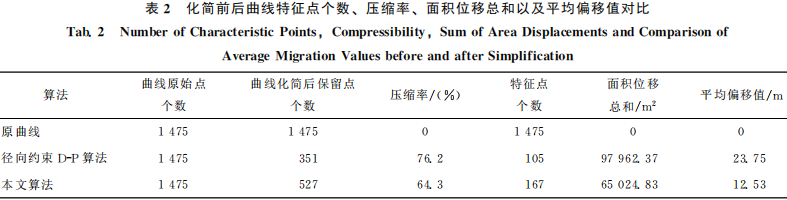
統計兩種壓縮 *** 下道路曲線簡前后保留點的個數、特征點個數、壓縮 率、面積位移總和以及平均偏移差[19-22]的對比情況，見表２。由圖５（ａ）和表２可知該道路曲線共有1475個點，當使用徑向約束D-P 算法進行曲線全局特征 點提取后，道路曲線全局保留點的數量為351個， 被化簡的點的數量為1124個，壓縮率達到76.2％，盡管壓縮率很高，但是提取曲線全局的特征點數量僅為105個，數量明顯偏少，曲線上一 些重要的特 征點沒有被保留下來，原因是在提取的過程中曲度較大處的一些特征點被忽略掉，同時面積位移總和為97962.37 ｍ2、平均偏移差為 23.75ｍ2都明顯偏大，導致化簡后相對位置發生較大變化，主要是由于垂距閾值的隨 機性導致曲線在曲度較大處造成一些重要特征點缺失，在彎曲的水平距離較短處造成非特征點的保留造成的。由圖５（ｂ）和表２可知在使用本文算法進行曲線全局特征點提取時，道路曲線全局保留點的數量為527個，被化簡 的點的數量為948個，壓縮率為 64.3％，提取曲線全局特征點的數量為167個，不論是保留點的個數還是特征點的個數均明顯多于徑向約束D-P算法提取的數量，壓縮率也超過了一半，同時面積位移總和為65024.83m2、平均位移差為12.53ｍ，都明顯低于傳統 *** ，本文 *** 通過比較各自的 標準差，選取各自更優的平均 數或中位數作為能否保留曲線特征點的參考值， 然后判斷曲線上每個點的彎曲程度與曲線整體彎曲程度的大小，用自適應來提取曲線的全局特征點。

２）以河流曲線進行實驗效果圖對比。圖６為 分別依據徑向約束D-P算法和本文 *** 提取河流曲線全局特征點的結果 。用D-P算法提取 河流曲線全局特征點的局部效果見圖６（ａ）；用 本文算法提取曲線全局特征點的局部效果， 見 圖６（ｂ）。

統計兩種壓縮 *** 下河流曲線化簡前后保留點的數量、特征點數量、壓縮率、面積位移總和、以及平均偏移差[19-22]的對比情況，見表３。

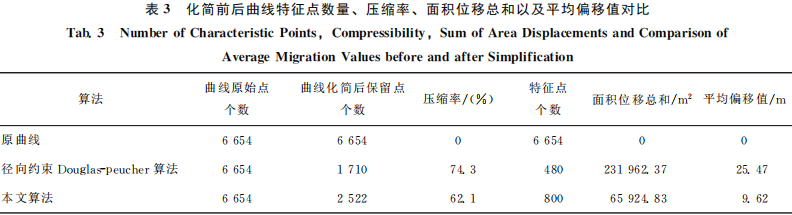
由圖6(a)和表３可知該河流曲線共有6654個點， 當使用徑向約D-P算法進行曲線全局特征點提 取后，河流曲線全局保留點的數量為1710個，被化簡的點的數量為4944個，壓縮率為74.3％，壓 縮率很高，但是提取曲線全局的特征點個數僅為480個， 數量明顯偏少， 同時面積位移總和為 231962.37m2、平均偏移差為25.47m都明顯偏大，導致一些交叉口處[22]、曲度較大處以及曲線 彎曲水平距離較短處的特征點化簡之后與原曲線 的相對位置誤差可能非常大，主要是由于垂距閾值的隨機性導致曲線在曲度較大處造成一些重要特征點缺 失，在彎曲的水平距離較短處造成非特 征點的保留造成的。由 圖6(b)和表３可知在使用本文算法進行曲線全局特征 點提取時，河流曲線全局保留點的數量為2522個，被化簡的點的數量 為4132個，壓縮率為62.1％，提取曲線全局特征 點的數量為800個，不論是保留點的個數還是特征 點的個數均明顯多于徑向約束D-P算法提取的 數量，壓縮率也超過了50％，同時面積位移總和為65924.83ｍ2、平均位移 差 為9.62ｍ都明顯低于傳統 *** ，因為本文通過標準差分別計算出間隔點連線 的參考值和中間點到該線垂線的參考值，通過比較曲線上每個點的彎曲程度與曲線整體彎 曲程度的大小，通過自適應來提取曲線的全局特征點。

曲線特征點的識別被廣泛用于反映河流等級化簡、道路化簡以及等高 線的化簡。線要素化簡算法的核心思想是在盡可能保持曲線形狀特征的前提下，盡量減少其節點的數量，所以準確提取特征點十分重要。對于道路、河流等曲線進行全局特征點提取時，傳統的徑向約束D-P算法提取的結果與原曲線誤差可能較大，主要是由于垂距 閾值的隨機性導致在曲度較大處易造成一些重要特征點缺失，在彎曲的水平距離較小處造成非特征點的保留。本文通過判斷曲線上每個點的彎曲程度，設計實現了一種改進的曲線特征點提取 *** ，通過比較曲線上每個點的彎曲程度與曲線整 體彎曲程度的大小，通過自適應來提取曲線的全局特征點，能夠較好地提取曲度較大處的一些重要特征點，同時能夠避免彎曲水平距離較小處一些非特征點的保留，從而更大可能保持與原曲線 形狀特征一致，所以本文算法更加符合實際的應用需求。