作者：辜聲峰

自上世紀八十年代GPS靜態長基線解算開始，高精度GNSS數據處理發展至今已三十余年。隨著實時GNSS高精度導航定位服務的普及，近年來PPP-RTK受到了國內外研究學者以及導航從業者的極大關注。本文結合筆者在實時GNSS高精度數據處理領域的相關工作，簡要介紹RTK、PPP與PPP-RTK的發展歷程，以及PPP-RTK目前進展情況，希望能夠對業界人士有一定的參考和借鑒，考慮到筆者知識與能力有限，文中難免出現錯誤和疏漏之處，懇請各位老師、專家不吝賜教。

 前  言  

移動互聯網的發展促進了導航與位置服務等新興產業的形成，我國北斗衛星導航系統、歐洲Galileo系統的建設，以及美國GPS、俄羅斯GLONASS等全球衛星導航系統的現代化進程為優質的導航與位置服務提供了新的契機1。

實時動態定位RTK（Real-Time Kinematic）以及精密單點定位PPP（Precise Point Positioning）是高精度衛星導航定位中應用最為廣泛、更具代表性的技術。RTK由差分定位技術發展而來，其原理是衛星軌道誤差、衛星鐘差、電離層延遲、對流層延遲等誤差對相距不遠的GNSS站影響接近，因此可以通過站間觀測值差分消除，進而實現相位模糊度的快速固定與瞬時厘米級定位。顯然，RTK技術需要架設基站，因此作業方式不靈活，成本也相對較高，而且隨著用戶與基準站距離的增加，其定位效果顯著降低。與之相對，PPP由非差定位技術發展而來，是一種全球尺度的定位技術，PPP通過全球分布的約100個基準站解算高精度衛星星歷產品修正用戶軌道、鐘差誤差等，即可獲得靜態毫米至厘米級，動態厘米至分米級的定位服務。然而如圖 1所示，與RTK瞬時厘米級相比，PPP需要近30分鐘才能實現精密定位的初始化，且信號失鎖后的重新初始化時間與首次初始化時間幾乎一樣長，因而限制了其在實時應用中的普及2。

微信號：MeetyXiao
添加微信好友, 獲取更多信息
復制微信號

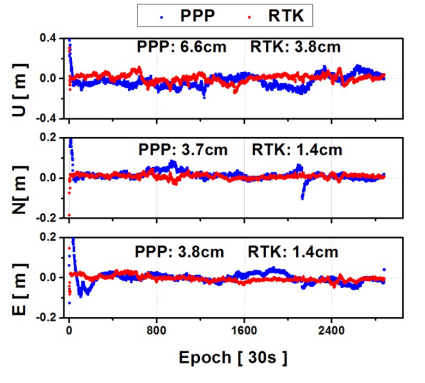
圖 1 RTK與PPP定位誤差時序圖

與專業用戶不同，用戶體驗是衡量導航與位置服務質量的重要因素之一，顯然，服務覆蓋范圍有限、近半小時等待時間都會讓用戶望而卻步。如何擴大RTK服務范圍、如何縮短PPP初始化時間成為困擾高精度GNSS導航定位服務從業者的主要問題3。

擴大RTK服務范圍方面，得益于 *** 與無線通訊技術的發展， *** RTK（NRTK）技術應運而生，與常規RTK單基站差分不同，NRTK通過組建連續運行參考站網系統CORS，結合基線處理與觀測值（改正數）內插技術，實現流動站實時動態高精度相對定位。NRTK技術雖然能提高作業靈活性、降低運行成本，而且一定程度上提高了覆蓋范圍，但也僅能滿足省市級CORS高精度定位服務4,5。例如我國就有多個省市就有自己獨立運維的CORS *** RTK服務。考慮更大范圍NRTK服務，隨著云計算與虛擬化技術的普及，通過 *** 統一管理和調度廣域分布（不同省市）的CORS，結合虛擬參考站VRS（Vritual Reference Station）等 *** 在技術上實現了RTK用戶跨省市CORS網的漫游6,7。有觀點認為RTK需要雙向通信，且需要將用戶坐標發送給服務端，這不僅進一步增加了數據傳輸壓力，同時不利用用戶隱私保護。但筆者認為RTK雙向通信只是為了和目前使用最廣泛的RTK服務模式VRS相兼容，實際上采用單向通信也能實現NRTK。該 *** 的真正問題在于：一方面依賴于密集基準站資源，當多個CORS網間存在覆蓋盲區時難以實現連續服務；另一方面采用“觀測值”的形式提供改正數，不同區域“觀測值”各異，因此對通信帶寬要求高，難以滿足星基廣播式增強服務需求。

縮短PPP初始化時間方面，相關學者通過仔細對比分析RTK和PPP數學模型，指出兩者的本質區別在于1）載波相位模糊度參數的整數固定以及2）高精度大氣延遲改正。那么，是否可以通過引入模糊度整數固定和大氣延遲增強，實現基于PPP模式的瞬時厘米級定位？Gabor和Nerem于1999年首次提出了單站PPP模糊度固定的算法與思想，然而受限于當時GPS的SA政策、衛星星歷等產品精度，并沒有達到理想效果，但一座連接PPP與RTK的橋梁就此浮現8。隨后，德國GFZ學者Ge等，法國CNES學者Laurichesse等，以及加拿大NRCan學者Collins等相繼提出相位小數偏差、整數鐘、去耦鐘等模型 *** ，不斷添磚加瓦并正式搭建起這座橋梁9,10,11,12。上述 *** 在PPP基礎上，實現了模糊度固定AR（Ambiguity Resolution），因此這類 *** 也常被稱為PPP-AR。考慮高精度大氣延遲改正在PPP中的應用，德國GEO++公司Wübbena等在2005年首次正式提出了PPP-RTK的概念，通過CORS網數據處理將GNSS各類誤差在“狀態域”建模，采用非差PPP實現與RTK相當的定位效果13。

值得說明的是，PPP與RTK“牽手成功”并不是單方面的。例如非差 *** RTK技術URTK即在一定程度上實現了差分與非差算法的兼容14,15。顯然，沿著這一思路并將其應用至全球也能實現“RTK-PPP”（若不是稱為PPP-RTK的話）。圖 2簡要給出了RTK、PPP以及PPP-RTK的發展歷程。可以看出，不論從RTK或PPP的角度，似乎都在朝著相同的方向發展，殊途同歸！

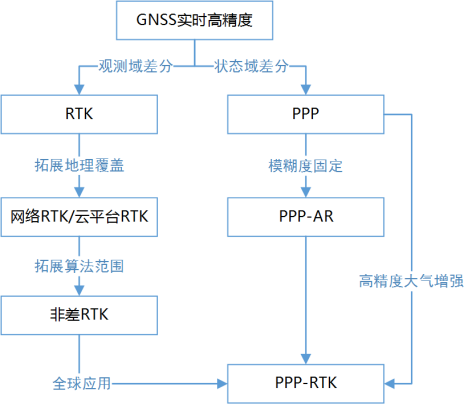
圖 2 RTK、PPP、PPP-RTK發展歷程

PPP-RTK通過狀態域建模，將基準站“觀測值誤差”分解為衛星軌道、衛星鐘差、衛星相位偏差、電離層延遲、對流程延遲等“狀態量誤差”，因此RTK和PPP/PPP-RTK也分別稱為“觀測值域差分”和“狀態域差分”。不嚴格的說，數學意義上可以認為衛星軌道、衛星鐘差、衛星相位偏差、電離層延遲、對流程延遲等狀態量誤差構成了GNSS觀測誤差空間的一組極大線性無關向量組，即構成了GNSS觀測誤差空間的一組基。該空間中任意向量，即觀測值誤差都可以認為是該組基向量的線性組合：基向量在對應衛星-接收機視線方向上的投影。

一個線性空間可以有無數組基（除零空間），所以GNSS觀測誤差空間一定也可以由其他基向量表達？是的，通過選取一組基準站“觀測值誤差”作為基向量，也能實現全球PPP-RTK服務。這不正是從NRTK，URTK走向PPP-RTK的方式嗎？從這個角度理解，天上衛星和地面基準站對于定位服務來說可能并沒有什么區別。然而與衛星軌道鐘差、相位偏差、大氣延遲這組基相比，“觀測值誤差”基向量的選擇并不容易：既要保證相互獨立，又要能張成整個空間（目前RTK觀測值域誤差向量即不相互獨立，也難以張成整個空間），更麻煩的是該組基如何投影至衛星-接收機視線方向并不直觀（別以為你能逃過定軌！）。

一組基能用最少的向量表達整個空間，因此相比于從觀測值域差分RTK，狀態域差分PPP-RTK能夠以較小的通訊帶寬實現廣域（甚至全球）服務覆蓋。

狀態域差分概念的提出為PPP-RTK提供了理論支撐。然而細心的讀者可能會問，衛星軌道鐘差、相位偏差可由狀態向量 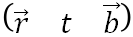表達，但大氣延遲呢？以電離層延遲為例，其狀態向量究竟是什么？雖然太陽F10.7指數、太陽黑子數、氧氮比、峰值密度、峰值高度、地磁指數等常用于表征電離層特征，或是將電離層延遲表達為一組球協或多項式系數，但由于電離層延遲的隨機性，上述狀態量都難以滿足PPP-RTK中厘米級電離層延遲改正需求16。實際處理中，不論電離層還是對流層延遲通常都采用一組離散化的時空采樣點描述。這么看來，PPP-RTK中大氣延遲改正倒更像是RTK中觀測值域誤差向量表達了，而且同樣存在數據量大，難以實現星基跨區域服務的難題。可以認為PPP-RTK中“PPP”體現在狀態域參數：衛星軌道鐘差、相位偏差等；“RTK”則體現在觀測域參數：電離層延遲、對流程延遲等。PPP-RTK也面臨不同區域“大氣延遲”各異，因此對通信帶寬要求高，難以滿足星基廣播式增強服務需求的挑戰。

既然如此，PPP-RTK相對于RTK究竟有何優勢？筆者認為，PPP-RTK從觀測值層面實現了PPP與RTK的“緊組合”，以一種更優雅的方式解決了RTK“依賴于密集基準站資源，當多個CORS網間存在覆蓋盲區時難以實現連續服務”的問題：有密集基準站與RTK相當、無密集基準站與PPP相當，無縫過渡。不優雅的方式？例如用戶同時運行PPP與RTK服務，并以兩者“松組合”作為最后輸出。

所以PPP-RTK僅僅只是更優雅？

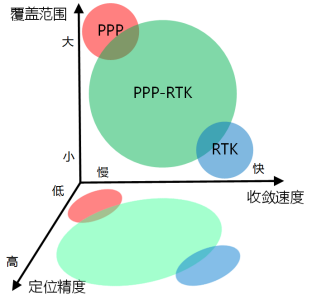
圖 3 RTK、PPP與PPP-RTK導航與位置服務模式對比

圖 3從收斂速度、定位精度、覆蓋范圍三個維度進一步對比了RTK、PPP以及PPP-RTK三種模式的導航與位置服務，可以認為RTK與PPP是PPP-RTK服務模式的特例或延伸，因此PPP-RTK具有較高的伸縮性。

等等，精度、收斂速度、覆蓋范圍是我們衡量導航定位服務性能的重要指標，伸縮性是指什么？彈性？對了，相比于RTK和PPP，PPP-RTK是一種更具彈性的服務模式，與楊元喜院士提出的彈性PNT服務體系更為契合17。PPP-RTK服務模式的彈性體現在，衛星軌道鐘差、相位偏差作為GNSS高精度定位的基礎，可采用狀態域表達實現星基增強服務，對于電離層延遲、對流層延遲增強，則可通過采樣頻率的調整以滿足不同參考站密度、不同播發帶寬、不同用戶性能需求。武漢大學學者張小紅等指出，同時兼顧模型精度與模型數據量的電離層延遲建模 *** 也是PPP-RTK需要解決的重要問題之一18。

目前，日本準天頂衛星系統（QZSS）已率先基于其L6D信號實現了星基PPP-RTK增強服務――CLAS(Centimeter Level Augmentation Service)，數據播發速率2000bps，服務范圍覆蓋日本本土19。此外，也有一些商業公司開始提供PPP-RTK服務，例如Trimble公司的CenterPoint RTX服務、NovAtel公司的TerraStar-X服務、Fugro公司的Marinestar G4+服務以及GEO++公司的SSRPOST服務等。雖然上述商業服務或多或少用到（至少借鑒）了PPP-RTK技術，但其電離層延遲模型表達、編碼格式、播發方案等都鮮有公開資料可供參考。

PPP作為北斗三號全球系統七大規劃公開服務類型之一，已利用三顆GEO衛星B2b信號I支路為中國及周邊地區用戶提供30分鐘內收斂的分米級免費服務，播發數據速率500bps，并預計將進一步增加播發帶寬，進一步提升精度，減少收斂時間20。顯然PPP-RTK成為潛在的升級方案。

為了驗證星基PPP-RTK定位精度與收斂速度，以及城市復雜環境下PPP-RTK/INS/VISION協同車載導航定位性能。筆者在FUSING（FUSing IN Gnss，復興）軟件基礎上，進一步實現了星基PPP-RTK模塊。目前FUSING軟件已涵蓋GNSS實時高精度定位服務各項功能，如多系統濾波定軌、精密鐘差估計、大氣延遲建模與監測以及多源協同精密定位等，并成功應用于武漢大學IGS實時分析中心產品服務21,22,23。

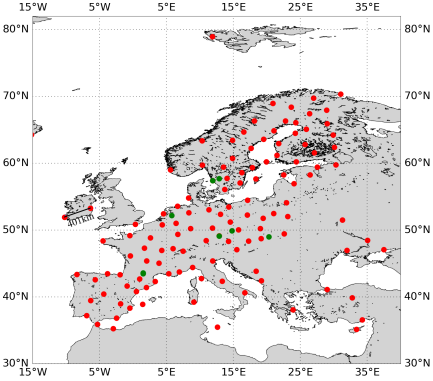
圖 4 歐洲區域星基PPP-RTK測站分布圖，紅色：117個基準站，相位偏差與電離層延遲解算；綠色：8個用戶站，PPP-RTK定位

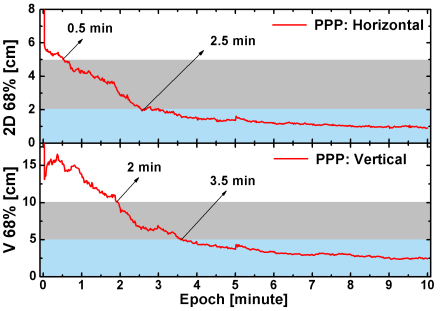
圖 5 歐洲區域星基PPP-RTK定位68%收斂時序圖（每10分鐘重啟，共1104個樣本）

首先模擬采用2000bps帶寬實現歐洲區域GPS、Galileo與GLONASS多系統PPP-RTK服務，實驗中各用戶站定位每10分鐘重啟。跟蹤站網分布如圖 4所示，定位68%收斂序列如圖 5所示。從圖中可以看出，采用星基多系統PPP-RTK，平面收斂至5厘米和2厘米分別需要0.5分鐘和2.5分鐘，高程收斂至10厘米和5厘米分別需要2分鐘和3.5分鐘，10分鐘后，平面和高程統計精度RMS分別為1厘米和2.5厘米。

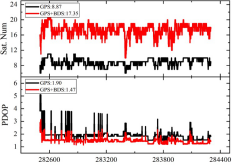
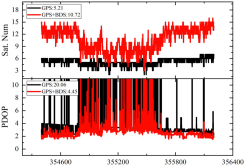
考慮PPP-RTK在城市環境下車載多源導航定位應用中的性能，下面我們給出了兩組實驗結果。傳感器包括北斗/GPS雙系統接收機、MEMS級慣導以及單目視覺相機。車輛行駛路徑、典型觀測環境以及衛星數與DOP值如圖 6所示。其中實驗一在武漢市郊展開，觀測環境較為開闊，主要受道路兩旁樹木遮擋。實驗二在武漢大學內部進行，樹木成蔭，部分路段幾乎完全被樹木遮擋。

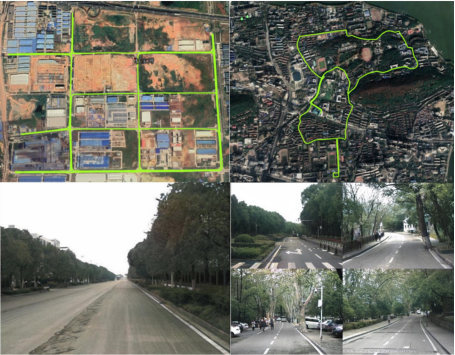
實驗一                          實驗二

圖 6 城市環境下PPP-RTK/INS/VISION多源導航實驗車輛行駛路徑以及典型觀測環境

圖 7和圖 8分別給出了兩組實驗定位誤差時序圖。通過對比可知，在實驗一較開闊環境下，PPP-RTK相對于PPP的精度提升顯著，而INS和視覺貢獻相對有限，其PPP-RTK/INS/VISION協同精密定位水平和高程RMS分別為0.06米，0.15米。然而對于實驗二，由于部分路段GNSS信號遮擋嚴重，此時無論PPP或PPP-RTK都只能提供1至2米的定位服務。當采用PPP-RTK/INS/VISION協同精密定位時，平面和高程RMS精度分別為0.56米，1.21米。

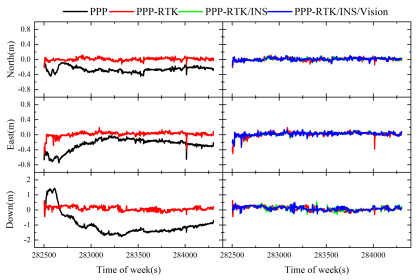
圖 7 實驗一PPP-RTK/INS/VISION多源車載定位誤差時序圖

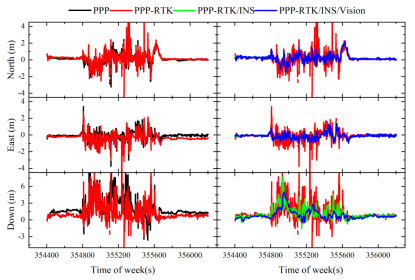
圖 8 實驗二PPP-RTK/INS/VISION多源車載定位誤差時序圖

瞬時厘米級是RTK主要優勢，全球低成本是PPP的主要優勢。PPP-RTK不僅從算法層面統一了RTK與PPP，在實際應用中也同時具備兩者優勢，而RTK與PPP分別可看作是PPP-RTK服務模式的特例或延伸。當跟蹤站網密度、播發帶寬相同時，PPP-RTK能分別達到（甚至優于）RTK和PPP各自導航定位性能。

PPP-RTK中“PPP”體現在狀態域參數：衛星軌道鐘差、相位偏差等，可由狀態向量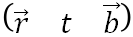表達，實現星基厘米級高精度增強；而PPP-RTK中“RTK”則體現在觀測域參數：電離層延遲、對流程延遲等，通常采用一組離散化的時空采樣點描述，同時可通過采樣頻率的調整以滿足不同參考站密度、不同播發帶寬、不同用戶性能需求。因此，相對于RTK和PPP,PPP-RTK是一種更具彈性的高精度導航定位服務模式。

本文采用FUSING軟件，實現了星基多系統PPP-RTK實驗驗證，結果表明平面收斂至5厘米和2厘米分別需要0.5分鐘和2.5分鐘，高程收斂至10厘米和5厘米分別需要2分鐘和3.5分鐘。而城市復雜環境下車載協同精密定位實驗表明，在GNSS觀測環境較為開闊時，PPP-RTK相對PPP定位性能提升明顯，而當GNSS信號遮擋嚴重時，無論PPP或PPP-RTK都只能提供1至2米的定位服務，此時只有采用PPP-RTK/INS/VISION協同精密定位，才可實現平面分米級定位。

參考文獻

[1]. Yang, Y., Xu, Y., Li, J., & Yang, C. (2018). Progress and performance eva luation of BeiDou global navigation satellite system: Data *** ysis based on BDS-3 demonstration system. Science China Earth Sciences, 61(5), 614?C624.http://doi.org/10.1007/s11430-017-9186-9

[2]. European GNSS Agency (2019). PPP-RTK market and technology report

[3]. 辜聲峰. (2013). 多頻GNSS非差非組合精密數據處理理論及其應用. 武漢大學，武漢

[4]. 施闖, 章紅平, 辜聲峰, 樓益棟, 唐衛明. (2015). 云定位技術及云定位服務平臺. 武漢大學學報?信息科學版, 1?C5. http://doi.org/10.13203/j.whugis20150118

[5]. 施闖,辜聲峰, 景貴飛,  耿江輝, 樓益棟, 唐衛明. (2019). 霧定位及其應用研究. 全球定位系統, 44(5), 1?C9. http://doi.org/10.13442/j.gnss.1008-9268.2019.05.001

[6]. Wübbena G., Bagge A., Seeber G., Boder V., Hankemeier P. (1996) Reducing distance dependent errors for real-time precise DGPS applications by establishing reference station networks, Proc 9th Int. Tech. Meeting of the Satellite Division of the U.S. Inst. of Navigation, Kansas City, ION GPS-96, September 17-20, 1845-1852.

[7].  Han S.W., Rizos C. (1996) GPS network design and error mitigation for real-time continuous array monitoring system, Proc 9th Int. Tech. Meeting of the Satellite Division of the U.S. Inst. of Navigation, Kansas City, Missouri, ION GPS-1996, September 17-20, 1827-1836.

[8]. Gabor MJ, Nerem RS (1999). GPS carrier phase ambiguity resolution using satellite-satellite single differences. In: Proceedings of ION GNSS 12th International Technical Meeting of the Satellite Division, Nashville, US, 1999, pp 1569-1578.

[9]. Ge, M., Gendt, G., Rothacher, M., Shi, C., & Liu, J. (2007). Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. Journal of Geodesy, 82(7), 389?C399. http://doi.org/10.1007/s00190-007-0187-4

[10]. Laurichesse D, Mercier F, Berthias JP, Broca P, Cerri L (2009) Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 56(2):135?C149

[11]. Collins P , Bisnath S , Lahaye F , et al (2010). Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing[J]. Navigation, 57(2):123?C135.

[12]. Teunissen, P. J. G., & Khodabandeh, A. (2014). Review and principles of PPP-RTK methods. Journal of Geodesy, 89(3), 217?C240. http://doi.org/10.1007/s00190-014-0771-3

[13]. Wübbena G, Schmitz M. Bagge A. PPP-RTK: Precise Point Positioning Using State-Space Representation in RTK Networks. ION GNSS 2005, Long Beach, California, U.S. September, 2005.

[14]. Wanninger L. (1995) Improved ambiguity resolution by regional differential modelling of the ionosphere, Proc 8th Int. Tech. Meeting of the Satellite Div. of the U.S. Institute of Navigation, Palm Springs, California, ION GPS-95, September 12-15, 55-62.

[15]. Zou, X., Ge, M., Tang, W. Shi, C., Liu, J. URTK: undifferenced network RTK positioning. GPS Solut 17, 283?C293 (2013). https://doi.org/10.1007/s10291-012-0277-5

[16]. Zhao, Q., Wang, Y. T., Gu, S., Zheng, F., Shi, C., Ge, M., & Schuh, H. (2019). Refining ionospheric delay modeling for undifferenced and uncombined GNSS data processing.Journal of Geodesy, 93(4), 545?C560. http://doi.org/10.1007/s00190-018-1180-9

[17]. 楊元喜. (2018). 彈性PNT基本架構. 測繪學報, 47(7), 893?C898.http://doi.org/10.11947/j.AGCS.2018.20180149

[18]. 張小紅, 胡家歡, 任曉東. (2020). PPP/PPP-RTK新進展與北斗/GNSS PPP定位性能比較. 測繪學報, 49(9), 1084?C1100. http://doi.org/10.11947/j.AGCS.2020.20200328

[19]. Cabinet Office (2018). Quasi-Zenith Satellite System Performance Standard (PS-QZSS-001)

[20]. 中國衛星導航系統管理辦公室 (2020). 北斗衛星導航系統空間信號接口控制文件精密單點定位服務信號PPP-B2b（1.0版）

[21]. Gong, X., Gu, S., Lou, Y., Zheng, F., Ge, M., & Liu, J. (2017). An efficient solution of real-time data processing for multi-GNSS network. Journal of Geodesy, 16(1), 1?C13.http://doi.org/10.1007/s00190-017-1095-x

[22]. Luo, X., Gu, S., Lou, Y., Cai, L., & Liu, Z. (2020). Amplitude scintillation index derived from C / N 0 measurements released by common geodetic GNSS receivers operating at 1 Hz. Journal of Geodesy, 94(2), 1?C14. http://doi.org/10.1007/s00190-020-01359-7

[23]. Gu, S., Wang, Y., Zhao, Q., Zheng, F., & Gong, X. (2020). BDS-3 differential code bias estimation with undifferenced uncombined model based on triple-frequency observation. Journal of Geodesy, 1?C13. http://doi.org/10.1007/s00190-020-01364-w