Topology—詞來自于希臘文,它的原意是“形狀的研究”。拓撲特性指在拓撲變換(任意伸縮或變形,但不扭結或折疊) 下能夠保持不變的幾何屬性。地理空間關系的研究所特別關注的 幾個重要拓撲特性是連接性、包含和鄰接性。
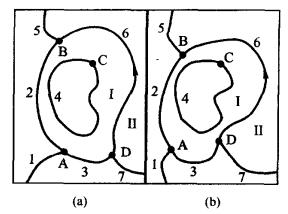
1.連接性。空間曲線的交點常稱為結點。連接性(connectivity)指曲線或弧段在結點處的相互聯接關系。在下圖中,圖a中的圖形較大幅度地變形為圖b所示,但是曲線或弧段的連接關系并不變化,例如,弧段1、2、3仍在結點4處連接;弧段2、5、6仍在結點B處連接。可見,“連接性”是一種拓撲特性。
2.包含。包含(inclusion)關系有時僅就多邊形或區域而言,但我們這里采用更廣泛的理解,將點、線、面之間能夠定義的 所有包含關系或組成關系,都納人包含的范疇。例如,一個點在一條線上或是其端點個點在一個區域或多邊形的邊界上或內部;一條線在一個多邊形內部;一個區域在另一個區域的內部等。比較上圖之a和b圖,可以證實這些空間關系在拓撲變換中皆保持不變。
位于一個較大區域內部的小區域,常稱為“島”。例如,下圖中,曲線4所圍的小區域,就是曲線2、3、6所聯合包圍的大區域中的一個“島”。

添加微信好友, 獲取更多信息
復制微信號
G1S中有兩種基本組成關系值得注意。其一,一條線可以者作由一連串點構成。如上述,地理信息系統中的曲線,實際上是由很多足夠小的線段組成的。因此,計算機中只要給出一條曲線所有線段之結點的坐標系列,就可以確定該曲線。其二,一個區域或一個多邊形由若干條線圍成,這種情況也稱為“多邊形區域定義”。例如,在上圖中,曲線2、3、4和6圍成了一個環狀區域,它們定義了多邊形I。在拓撲變換中,盡管形狀變化,但這個環狀區域由曲線2、3、4和6圍成這一特性也是不變的。
鄰接性。鄰接性(contiguity)指共有公共邊的兩個區域的鄰接關系,如上圖中,以曲線6為公共邊的多邊形I和n,就是相鄰接的區域。這種鄰接性也不會因拓撲變換而改變。
如果給公共邊指定方向,鄰接性還可以進一步描述為“右鄰”還是 “左鄰”。例如,上圖中,假定我們指定曲線6采取圖中所示的方向,那么,順該方向看,多邊形I就是左鄰,或左多邊形,多邊形Ⅱ就是右鄰,或右多邊形。如果曲線6的走向反轉,那么,左鄰與右鄰關系也要顛倒過來。
來源:開源地理空間基金會中文分會
來源鏈接:https://www.osgeo.cn/post/1e725
本站聲明:網站內容來源于 *** ,如有侵權,請聯系我們,我們將及時處理。








