多系統非差非組合精密單點定位電離層延遲約束權陣的確定
張輝 , 郝金明 , 謝建濤 , 劉偉平 , 周陽林
信息工程大學導航與空天目標工程學院, 河南 鄭州 450001
之一作者簡介:張輝(1989-), 男, 博士生, 研究方向為多系統GNSS精密定位。E-mail:zh_ljpd@163.com

添加微信好友, 獲取更多信息
復制微信號
摘要:非差非組合精密單點定位需要估計電離層延遲參數,采用電離層先驗改正模型約束可以輔助電離層參數解算。針對先驗電離層改正量與實際觀測量之間權比關系難以確定的問題,本文提出一種電離層約束權因子搜索算法,采用權因子對先驗電離層改正量的方差進行調整,根據驗后殘差加權平方和最小原則通過搜索找出較優的權因子,利用驗后殘差動態調整先驗電離層改正量的方差從而達到改善定位結果的目的。采用8個MGEX跟蹤站的GPS/BDS觀測數據對該算法進行驗證。靜態結果表明:對比傳統約束 *** ,采用搜索算法后平均三維定位精度由3.96 cm提高到3.40 cm,平均收斂時間由76.3 min縮短為59.9 min。
關鍵詞:多系統 精密單點定位 原始觀測量 全球電離層圖 電離層延遲約束
The Weight Matrix Determination of Ionospheric Delay Constraintfor Multi-GNSS Precise Point Positioning Using Raw Observations
ZHANG Hui , HAO Jinming , XIE Jiantao , LIU Weiping , ZHOU Yanglin
Abstract: The ionospheric delay parameters in the precise point positioning (PPP) using raw observations must be considered.The estimation of the ionospheric delay parameters is strengthened by priori ionospheric correction models. But it is difficult to determine the relative weight ratios between the priori ionospheric corrections and the observations. A weight factor searching algorithm based on ionospheric delay constraint for multi-GNSS PPP using raw observations is proposed in which weight factors are utilized to adjust the variances of priori ionospheric corrections. According to the principle thatthe sum of the quadratic forms of weighted residuals be the minimum, the optimal weight factors are searched for and the variances of priori ionospheric corrections are adjusted dynamically in order to promote the positioning results. Data sets collected from 8 stations of the multi-GNSS experiment (MGEX) tracking network are processed to validate the proposed algorithm. The results of PPP in static mode show that the RMS values of the positioning errors are improved from 3.96 cm to 3.40 cm andthe convergence time is reduced from 76.3 min to 59.9 min whenthe searching algorithm is used, in comparison with the traditional priori ionospheric constraint.
Key words: multi-constellation precise point positioning raw observations global ionospheric map ionospheric delay constraint
BDS系統在2012年宣布正式提供區域服務后發展迅速, 預計于2020年建成覆蓋全球的衛星導航系統[1]。隨著全球導航衛星系統(global navigation satellite system, GNSS)的快速發展, 多系統精密單點定位(precise point positioning, PPP)體現出顯著的優勢, 已經成為當前的研究熱點[2-11]。在多系統條件下, 非差非組合PPP處理多頻數據更為靈活, 避免了觀測量組合引起的噪聲放大, 并且可以獲得電離層延遲估計值, 有助于電離層建模研究[12-17]。因此, 研究多系統非差非組合PPP電離層延遲參數處理 *** 對于提高PPP的定位性能和電離層建模研究具有重要意義。
全球電離層圖(global ionospheric map, GIM)的相關科研成果為進一步研究GNSS電離層延遲誤差提供了有力支持。文獻[18]研究了總電子含量(total electron content, TEC)參數和電離層圖預測 *** , 并對歐洲定軌中心(Center for Orbit Determination in European, CODE)提供的電離層圖進行了驗證。文獻[19]總結了垂直總電子含量(vertical total electron content, VTEC)圖的生成 *** , 驗證了VTEC圖的可用性和典型VTEC變化周期。在此基礎上不少學者開展了利用電離層先驗改正模型提高GNSS定位性能的研究。文獻[20]通過試驗分析了電離層先驗改正模型對單頻GPS接收機的有效性并推薦采用GIM模型。文獻[21]驗證了利用區域電離層圖提高單頻PPP定位精度的可行性。文獻[22]提出一種歷元差分電離層延遲模型, 使用該電離層延遲模型能夠將單頻數據轉換成雙頻數據, 有助于單頻接收機估計對流層天頂延遲。文獻[23]研究了非差非組合PPP電離層參數處理 *** , 在使用電離層先驗改正模型約束的基礎上, 提出利用二階平穩過程的變異函數描述電離層隨機參數在歷元間的相關性, 該 *** 可以提高單頻PPP定位精度和收斂時間。文獻[24]提出一種區域電離層建模 *** , 該 *** 對每顆衛星的電離層延遲進行建模, 能夠提高單頻PPP定位精度和縮短雙頻PPP收斂時間。文獻[25]采用電離層空間約束和電離層先驗改正模型約束的 *** 進行了多系統非差非組合PPP試驗, 結果表明多系統PPP能夠有效縮短收斂時間和提高定位精度。
GIM電離層延遲改正量的精度較低, 一般僅有2~8 TECU(total electron content unit)[16], 傳統電離層約束 *** 難以確定電離層先驗改正量與實際觀測量之間合適的權比關系。利用GIM進行電離層延遲約束時, 如果電離層先驗改正量和實際觀測量的權比配置不合理會對平差結果造成負面影響。本文提出一種電離層約束權因子搜索算法, 采用權因子對先驗電離層改正量的方差進行調整, 根據驗后殘差加權平方和最小原則通過搜索找出較優的權因子。試驗結果表明, 搜索算法可以提高靜態PPP定位精度和收斂速度。
1 數學模型
采用精密衛星鐘差和差分碼偏差(differential code bias, DCB)產品消除衛星鐘差和衛星碼硬件延遲后, 基于原始觀測量的GPS/BDS精密單點定位偽距和相位觀測方程可以表示為
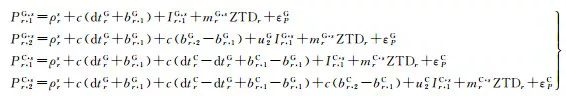 (1)
(1)
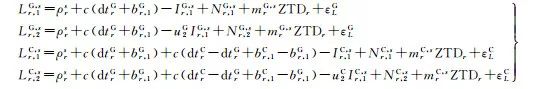 (2)
(2)
式中, 上標G和C分別表示GPS和BDS系統, 為方便敘述用上標T統一表示GPS和BDS系統; f為衛星信號的頻率; Pr, fT, s和Lr, fT, s分別為接收機r和衛星s在頻率f上的偽距和相位觀測量, 單位為m; ρrs為衛星s天線相位中心至接收機r天線相位中心的幾何距離; c為光在真空中的速度; dtrT為接收機鐘差; br, fT為頻率f上的接收機碼硬件延遲; Ir, 1T, s=FrsIvr, 1T, s為衛星s在第1個頻率上的斜電離層延遲, 可以用投影函數Frs和穿刺點處垂直電離層延遲Ivr, 1T, s的乘積表示, 實際參與平差的待估參數為Ivr, 1T, s; u2T=(λ2T/λ1T)2為頻率相關的比例因子; λfT為頻率f上的波長; ZTDr為接收機r的天頂對流層延遲; mrT, s為對流層延遲映射函數; Nr, fT, s為頻率f上的相位模糊度, 模糊度吸收了相位硬件延遲和衛星碼硬件延遲以及第1個頻率上的接收機碼硬件延遲br, 1T, 單位為m; εPT和εLT分別為偽距和相位觀測誤差包括觀測噪聲和多路徑誤差。
對式(1)和式(2)的參數進行合并, 新的參數可以表示為
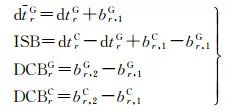 (3)
(3)
式中, dtrG為包含了偏差項的GPS接收機鐘差; ISB為BDS相對GPS的系統間偏差, DCBrT為接收機差分碼偏差。式(3)隱含的約束條件是令第1個頻率上的接收機碼硬件延遲br, 1T為零, 使其與接收機鐘差dtrT合并。該模型改正了衛星端偽距硬件延遲, 分別估計接收機端偽距DCB和電離層參數, 使得估計出的電離層參數不再受硬件延遲的影響, 為電離層建模及附有電離層約束的PPP提供了一種新的參數估計 *** 。
1.1 傳統電離層先驗改正模型約束 ***
CODE提供的GIM每1 h給出1幅TEC圖, 定義了格網點處的垂直方向總電子含量, 通過內插計算可以得到穿刺點處的垂直電離層延遲改正量。將GIM給出的垂直電離層延遲改正量作為虛擬觀測量引入平差系統, 虛擬觀測量的觀測方程可以表示為
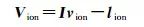 (4)
(4)
 (5)
(5)
式中, Vion為虛擬觀測量殘差向量; Ivion=[Ivr, 1T, 1Ivr, 1T, 2…Ivr, 1T, s]為垂直電離層延遲參數向量, 上標s為該歷元的衛星數; lion為垂直電離層延遲虛擬觀測量向量; DIion為虛擬觀測量的方差陣; σion2, s=σVTEC2(40.28×1016/(f1s)2)2為虛擬觀測量的方差; f1s為衛星s的第1個頻率; σVTEC2為穿刺點處垂直方向總電子含量的方差。
1.2 電離層約束權因子搜索算法
電離層約束權因子搜索算法的基本思路是, 在傳統電離層先驗改正模型約束的基礎上, 使用權因子對電離層虛擬觀測量的方差陣進行調整, 采用該方差陣進行電離層延遲約束和平差計算, 以驗后殘差加權平方和最小為原則通過搜索找出較優的權因子, 利用驗后殘差動態調整電離層虛擬觀測量的方差從而達到改善定位結果的目的。
搜索算法的具體流程為:第1步, 首次搜索時權因子從k=1開始; 第2步, 用權因子k乘以虛擬觀測量方差陣, 采用該方差陣進行電離層延遲約束; 第3步, 在平差計算后記錄下驗后殘差加權平方和的大小, 權因子k按搜索步長累加, 搜索步長為1;重復第2—3步直到找出搜索區間內驗后殘差加權平方和最小的權因子k, 利用該權因子得到的平差結果即為本歷元的最終結果。下一歷元從第1步開始重復該過程。驗后殘差加權平方和最小原則可以表示為
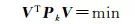 (6)
(6)
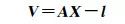 (7)
(7)
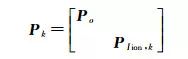 (8)
(8)
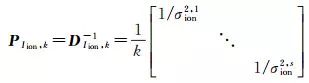 (9)
(9)
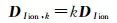 (10)
(10)
式中, V為實際觀測量和虛擬觀測量的殘差向量; A為設計矩陣; X為待估參數向量; l為實際觀測量和虛擬觀測量; Pk為所有觀測量的權陣包括實際觀測量權陣Po和虛擬觀測量權陣PIion, k; DIion, k為虛擬觀測量方差陣DIion和權因子k相乘得到的方差陣。設單位權方差為1, 由于DIion, k為正定對角矩陣, PIion, k可以直接由DIion, k求逆獲得。實際觀測量的方差由高度角相關模型確定σo2=a2+a2/sin2(E), σo2為實際觀測量的方差, E為衛星高度角, 對于偽距觀測量a=0.6 m, 對于相位觀測量a=0.003 m[26]。
為確定高效的權因子搜索區間, 對權因子與驗后殘差加權平方和的關系進行試驗分析, 試驗結果見圖 1。由圖 1可知, 隨著權因子的增加, 驗后殘差加權平方和逐步減小然后趨于平穩, 在收斂后如果權因子繼續增加, 加權平方和的變化并不明顯。由于GIM電離層延遲改正量的精度較低, 如果給定的改正量方差過小會導致驗后殘差增大。隨著權因子的增加, 外部約束逐步減弱, 通過搜索算法得到虛擬觀測量與實際觀測量較優的權比關系后, 驗后殘差加權平方和趨于穩定。為了提高搜索效率, 在加權平方和收斂后停止搜索, 較優權因子為最后一次搜索時的數值, 設置收斂標準為相鄰殘差加權平方和的變化小于0.5 m。圖 2給出了電離層約束權因子搜索算法的整體流程。此外, 由于殘差二次型易受粗差的影響, 采用搜索算法時需進行粗差探測, 剔除受到粗差影響的觀測量。
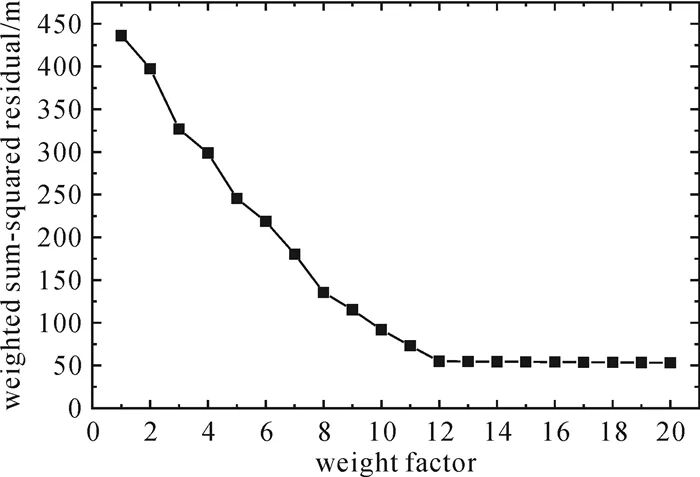
圖 1 權因子與驗后殘差加權平方和的關系Fig. 1 Relationships between the weight factors and the weighted sum-squared residuals
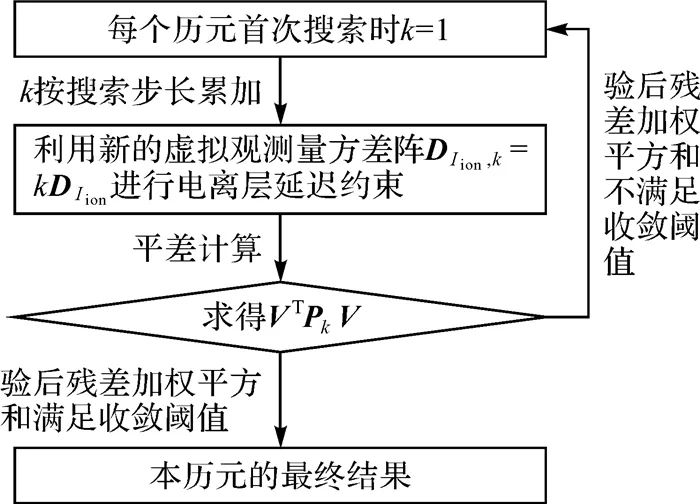 圖 2 電離層約束權因子搜索算法流程 Fig. 2 Flow chart for the weight factor searching algorithm based on ionospheric delay constraint
圖 2 電離層約束權因子搜索算法流程 Fig. 2 Flow chart for the weight factor searching algorithm based on ionospheric delay constraint
2 試驗與分析
為驗證算法的有效性, 采用8個MGEX跟蹤站(CUT0、KRGG、MOBS、NNOR、PERT、UCAL、YAR2和YEL2)2016年年積日21 d的數據進行試驗。使用3種試驗方案進行對比分析, 3種方案均使用GPS/BDS雙頻原始觀測量, 數據處理策略基本相同, 詳見表 1, 僅在電離層參數約束 *** 上有所區別:
表 1 數據處理策略Tab. 1 Strategies for the data processing of PPP
| 類別 | 處理策略 |
| 觀測量 | GPS+BDS偽距和相位原始觀測量 |
| 估計 *** | 卡爾曼濾波 |
| 信號 | GPS:L1, L2;BDS:B1, B2 |
| 采樣間隔 | 30 s |
| 截止角 | 7° |
| 觀測值加權 | 采用高度角定權模型 |
| 衛星天線相位中心 | GPS的PCO和PCV采用IGS08.ATX提供的改正值; BDS的PCO和PCV采用ESA提供的改正值 |
| 接收機天線相位中心 | GPS的PCO和PCV采用IGS08.ATX提供的改正值; BDS采用與GPS相同的PCO和PCV改正值 |
| 相位纏繞 | 改正 |
| 潮汐效應 | 改正固體潮、海潮和極潮 |
| 衛星軌道和鐘差 | 采用GFZ提供的精密軌道和精密鐘差產品 |
| 衛星差分碼偏差 | 采用MGEX提供的產品 |
| 對流層延遲 | Saastamoinen模型和隨機游走過程 |
| 電離層延遲 | 作為白噪聲估計 |
| 全球電離層圖 | 采用CODE提供的GIM產品 |
| 接收機坐標 | 作為常數估計 |
| 接收機鐘差 | 作為白噪聲估計 |
| 接收機ISB | 在一天中作為常數估計 |
| 接收機DCB | 在一天中作為常數估計 |
| 模糊度 | 在連續弧段作為常數估計, 采用浮點解 |
方案1, 不采用電離層約束(簡稱為無約束 *** )。
方案2, 采用傳統電離層先驗改正模型約束 *** (簡稱為傳統約束 *** )。
方案3, 采用本文提出的電離層約束權因子搜索算法(簡稱為搜索算法)。
接收機DCB在靜態模式下的估計精度較高, 因此選擇進行靜態PPP試驗。試驗分析部分從定位精度、收斂時間和接收機DCB估計精度三方面進行了詳細分析。收斂標準為水平和高程定位精度均優于0.1 m, 對收斂后定位誤差的均方根誤差(root mean square, RMS)進行統計。以IGS發布的DCB產品作為接收機DCB參考值, 統計了接收機DCB估計值與參考值的差值。
表 2對比了不同方案試驗結果, 圖 3給出了測站三維定位精度。由表 2可知, 無電離層約束 *** 的平均三維定位精度為4.19 cm。由圖 3可知, 與無電離層約束相比, 傳統約束 *** 的定位精度改進較小, 平均三維定位精度為3.96 cm, 而搜索算法的定位精度明顯提高, 平均三維定位精度為3.40 cm。采用傳統約束 *** 時, 部分測站的東向和北向定位精度變差, 東向平均定位精度由2.02 cm降低為2.14 cm。電離層延遲變化與空間水平梯度和電離層活躍程度密切相關, 因此GIM模型精度受到了一定限制[27]。由于GIM的精度較低, 僅為2~8 TECU, 在進行電離層約束時如果給定的電離層虛擬觀測量的方差過小, 可能會引入較大誤差。GIM模型誤差和投影函數誤差是部分分量定位精度變差的主要原因。圖 4給出了搜索算法確定的權因子。由圖 4可知, 權因子在不同歷元能夠動態調整, 基本穩定在2~6, 搜索算法采用的虛擬觀測量方差大于傳統約束 *** 。根據驗后殘差加權平方和最小原則, 采用搜索算法動態調整虛擬觀測量方差的大小可以避免外部約束引起的殘差過大, 對于改善平差結果具有顯著作用。
表 2 3種方案的PPP試驗結果Tab. 2 PPP solutions for the three strategies
| 測站 | 無約束 | 傳統約束 | 搜索算法 | |||||||||||
| E/cm | N/cm | U/cm | 收斂時間/min | E/cm | N/cm | U/cm | 收斂時間/min | E/cm | N/cm | U/cm | 收斂時間/min | |||
| CUT0 | 1.32 | 1.69 | 1.56 | 29.0 | 1.27 | 1.89 | 1.49 | 38.5 | 1.16 | 0.82 | 0.96 | 26.5 | ||
| KRGG | 1.75 | 3.46 | 2.96 | 181.5 | 2.22 | 2.82 | 1.21 | 158.0 | 1.81 | 2.92 | 1.33 | 155.0 | ||
| MOBS | 2.44 | 2.10 | 4.17 | 20.5 | 2.61 | 2.39 | 3.32 | 26.0 | 2.28 | 2.03 | 3.55 | 11.0 | ||
| NNOR | 0.99 | 1.58 | 3.62 | 16.5 | 1.77 | 1.47 | 3.39 | 22.5 | 1.18 | 0.61 | 2.52 | 15.5 | ||
| PERT | 2.31 | 1.49 | 1.75 | 24.0 | 1.18 | 1.28 | 1.86 | 36.5 | 1.41 | 0.70 | 1.56 | 26.5 | ||
| UCAL | 2.03 | 0.85 | 2.98 | 116.5 | 2.56 | 1.14 | 2.17 | 105.5 | 2.15 | 0.91 | 2.42 | 88.0 | ||
| YAR2 | 2.00 | 1.35 | 3.04 | 27.0 | 3.53 | 0.97 | 3.42 | 9.0 | 2.21 | 0.53 | 2.76 | 6.5 | ||
| YEL2 | 3.32 | 4.62 | 0.99 | 207.5 | 1.94 | 3.44 | 3.32 | 214.0 | 1.35 | 4.51 | 1.97 | 150.5 | ||
| 平均 | 2.02 | 2.14 | 2.63 | 77.8 | 2.14 | 1.93 | 2.52 | 76.3 | 1.69 | 1.63 | 2.13 | 59.9 | ||
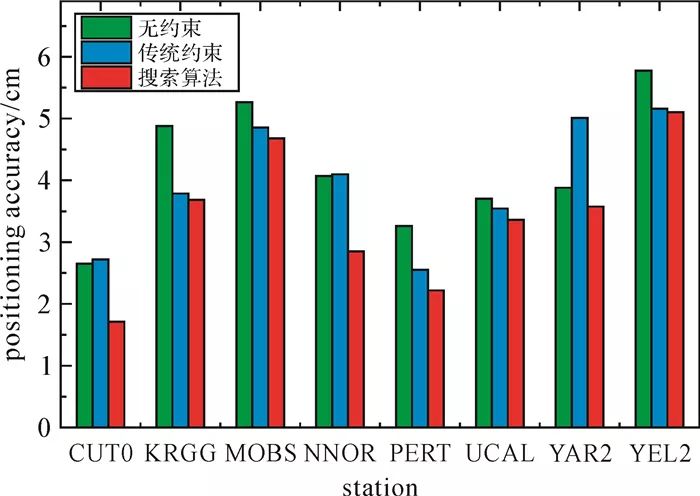
圖 3 3種方案的三維定位精度Fig. 3 3D positioning accuracies of PPP for the three strategies
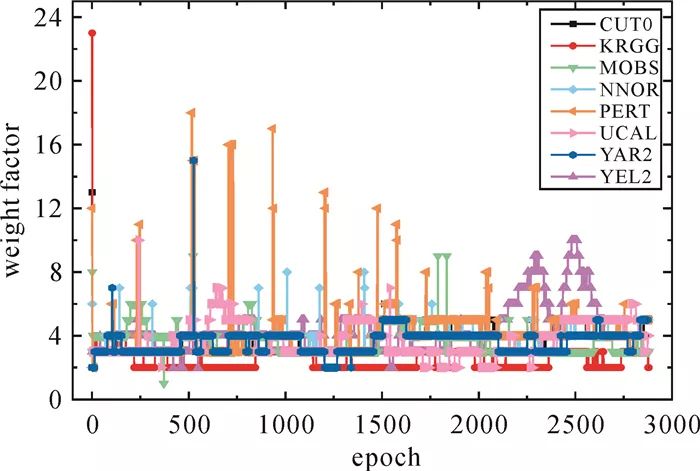
圖 4 搜索算法確定的權因子Fig. 4 Weight factors generated by the searching algorithm
圖 5給出了不同方案單天解的收斂時間。由圖 5可知, 無電離層約束的平均收斂時間為77.8 min。與無電離層約束相比, 傳統約束 *** 的改進較小, 平均收斂時間為76.3 min, 而搜索算法的收斂時間明顯縮短, 平均收斂時間為59.9 min。電離層延遲約束為卡爾曼濾波提供了更多的新息向量, 搜索算法確定了虛擬觀測量與實際觀測量之間較優的權比關系, 二者可以加快狀態參數分離, 提高收斂速度。為進一步驗證傳統約束 *** 和搜索算法在不同時段的收斂性能, 每隔4 h重置一次卡爾曼濾波器, 將一天分為6個時段, 對多時段的平均收斂時間進行統計。各測站多時段結果表明, 采用搜索算法后平均收斂時間由87.2 min縮短為68.6 min。以CUT0站為例, 圖 6給出了多時段PPP收斂過程。由圖 6可知, 搜索算法的收斂速度優于傳統約束 *** , 且各個時段的收斂時間并不相同, 其中第4時段(12:00—16:00)的收斂時間最長, 原因是電離層在地方時14:00左右最為活躍, 該時段GIM的改正效率較低。

圖 5 不同方案單天解的收斂時間Fig. 5 PPP convergence time of daily solutions with different strategies
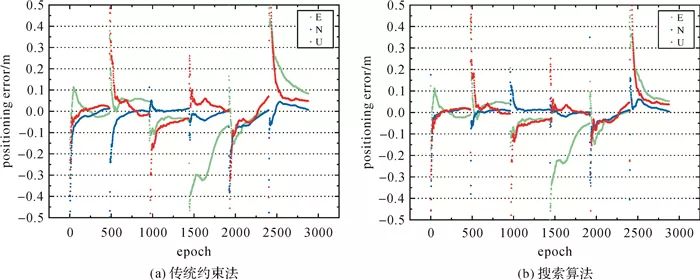
圖 6 CUT0站多時段PPP收斂過程Fig. 6 PPP convergence processin different time periodsat station CUT0
表 3給出了接收機DCB估計精度。當無電離層約束時, GPS-DCB和BDS-DCB的平均估計精度分別為1.49 ns和0.96 ns。傳統約束 *** 的GPS-DCB和BDS-DCB平均估計精度分別為0.56 ns和0.68 ns, 搜索算法的GPS-DCB和BDS-DCB平均估計精度分別為0.53 ns和0.65 ns。IGS提供的接收機DCB參考值浮動范圍約為1.0 ns[28]。3種 *** 接收機DCB平均估計精度的差異均小于1.0 ns, 處于參考值的浮動范圍內。搜索算法和傳統約束 *** 的DCB估計精度基本相當, 略優于無約束 *** 。
表 3 接收機DCB估計精度Tab. 3 Accuracy of the receiver DCB estimated by PPP
| ns | |||||||
| 測站 | GPS-DCB | BDS-DCB | |||||
| 無約束 | 傳統約束 | 搜索算法 | 無約束 | 傳統約束 | 搜索算法 | ||
| CUT0 | 1.96 | 0.64 | 0.59 | 0.48 | 0.61 | 0.61 | |
| KRGG | 0.92 | 0.81 | 0.70 | 0.58 | 0.80 | 0.77 | |
| MOBS | 2.12 | 0.44 | 0.49 | 2.17 | 0.25 | 0.27 | |
| NNOR | 2.12 | 0.36 | 0.31 | 0.20 | 0.50 | 0.48 | |
| PERT | 2.05 | 0.53 | 0.48 | 0.59 | 0.47 | 0.47 | |
| UCAL | 1.12 | 0.42 | 0.43 | 1.90 | 1.07 | 0.84 | |
| YAR2 | 1.59 | 0.49 | 0.45 | 0.68 | 0.67 | 0.66 | |
| YEL2 | 0.06 | 0.78 | 0.78 | 1.06 | 1.10 | 1.10 | |
| 平均 | 1.49 | 0.56 | 0.53 | 0.96 | 0.68 | 0.65 | |
3 結論
電離層先驗改正模型約束是非差非組合PPP常用的電離層參數處理 *** 。針對GIM電離層改正量與實際觀測量之間權比關系難以確定的問題, 本文提出一種電離層約束權因子搜索算法, 利用權因子對先驗電離層改正量的方差陣進行調整, 使用該方差陣進行電離層延遲約束, 以驗后殘差加權平方和最小為原則通過搜索找出較優的權因子。采用8個MGEX跟蹤站的GPS/BDS觀測數據對該算法進行驗證。靜態試驗結果表明:對比傳統約束 *** , 采用搜索算法后平均三維定位精度由3.96 cm提高到3.40 cm, 平均收斂時間由76.3 min縮短為59.9 min。
在非組合PPP電離層約束中, 要根據電離層改正模型精度進行合理定權。將先驗電離層改正量作為虛擬觀測量引入平差系統, 可認為實際觀測量和虛擬觀測量為兩類觀測量。搜索算法借鑒了方差分量估計 *** 的基本思想, 是該 *** 的一種簡化形式。搜索算法的步驟較為簡單, 具有易于實現、穩定性好的優點, 但缺點是搜索耗時較多, 占用計算資源。
【引文格式】張輝, 郝金明, 謝建濤, 等. 多系統非差非組合精密單點定位電離層延遲約束權陣的確定[J]. 測繪學報,2018,47(3):308-315. DOI: 10.11947/j.AGCS.2018.20170151








