前段時間,我又嘗試用TerraPos處理一下SeaPath330的原始姿態和定位數據,看看反演潮位的效果如何。
首先,怎么預處理SeaPath330的定位和姿態數據,
記錄格式如下1901200054.l09和1901200054.l10,咨詢了SeaPath330的技術張工,對話如下:
張工,有個問題咨詢一下,Seapath記錄的RTCM數據格式.l09和IMU原始數據.l10怎么轉成rinex和imu格式?

添加微信好友, 獲取更多信息
復制微信號
l10本身就是imu格式
l09 是rtcm,要轉成 rinex
rinex
直接改成imu可以嗎?
對
l09改成rtcm?
L09 用這個轉RInex
rinexconv.exe" -r 1 ***.rtcm > xxx.obs
-r 1 是之一個 天線 -r 2 是第二個
1是主天線嗎?
就是位置天線?
對
朝船后的那個天線是天線1?
要查一下
船后的那個天線是天線1
張工,在處理慣導的數據的時候,出現這樣的問題,
Initializing heading from velocity
No periods with suitable velocities found.
No periods with zero cross-track acceleration found.
張工,記錄的gps和imu原始數據的位置是nrp(重心)?還是各自位置的?
各自的中心
heave值也是mru5處的?
對的
除了張工使用的命令程序以外,也可以用GUI方式轉(推薦使用)
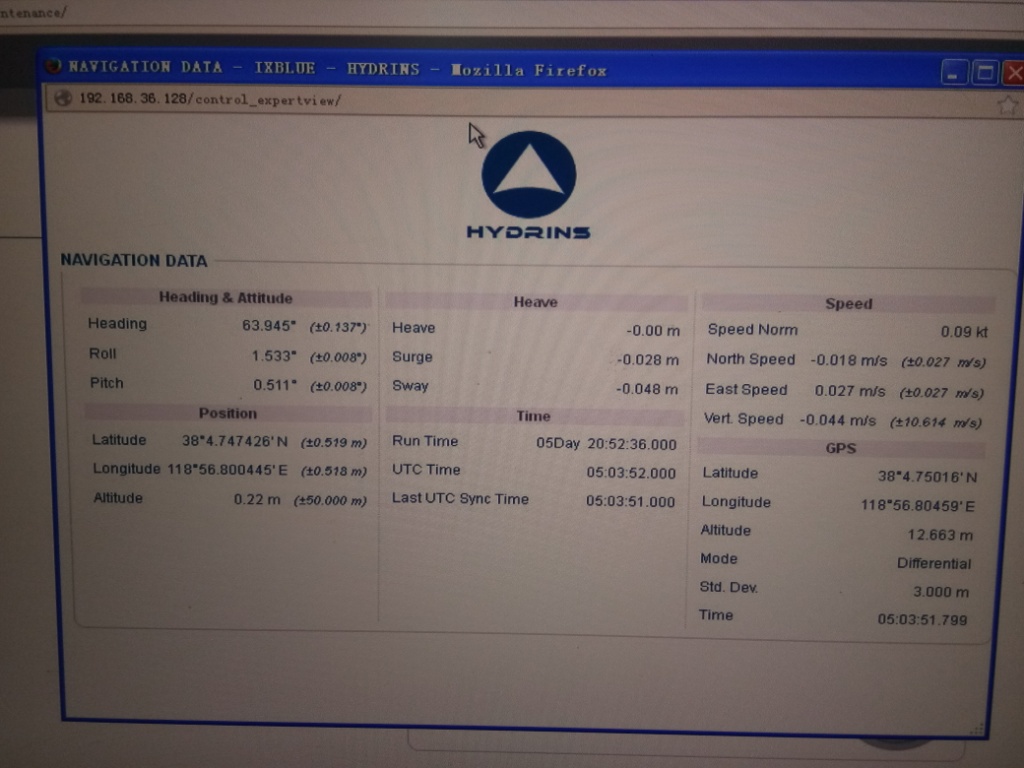
然后處理SeaPath的姿態和定位數據
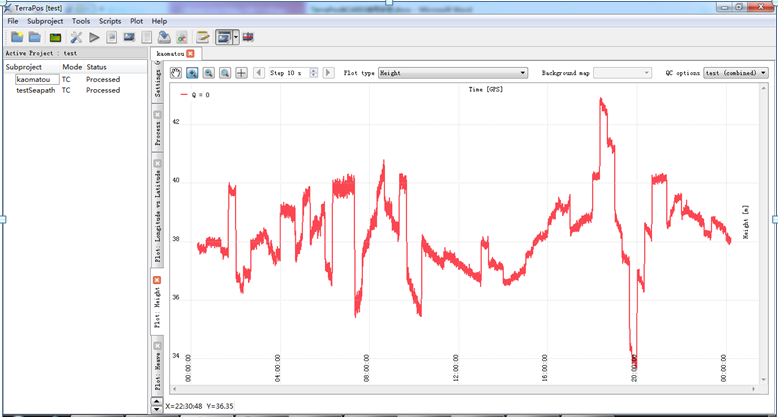
選取當船在碼頭的時候,差分信號不好
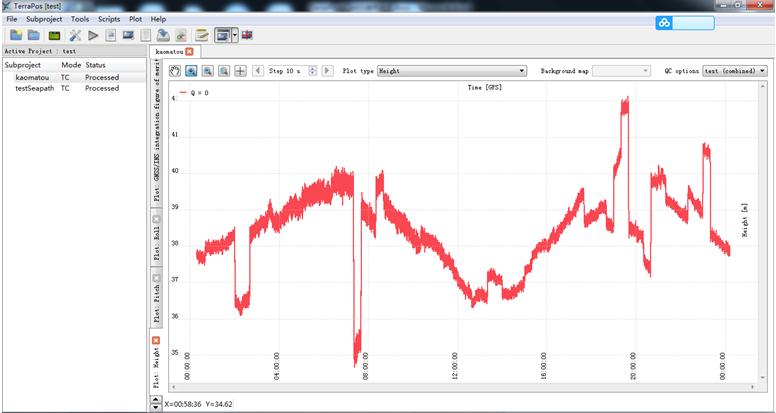
采用TC模式,用10s 卡爾曼濾波,下圖是高程曲線,效果有點慘不忍睹
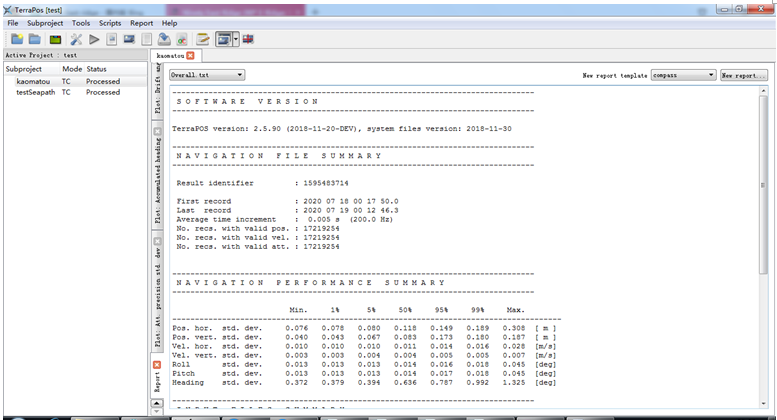
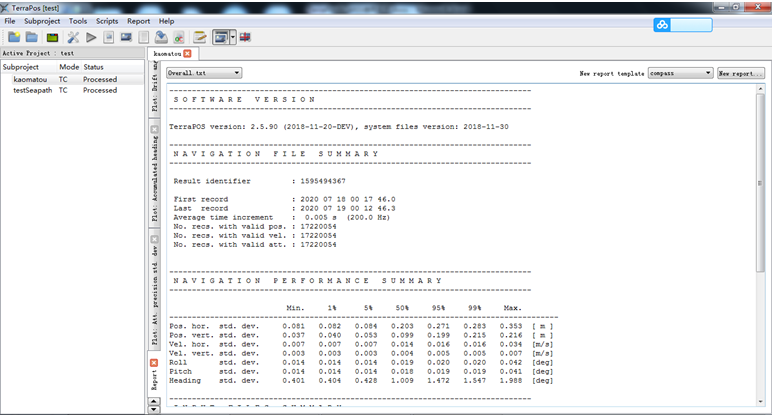
查看精度文件overall.txt,發現置信水平為95%時,高程誤差為17.3cm,這個效果一般,沒有達到10cm以內。
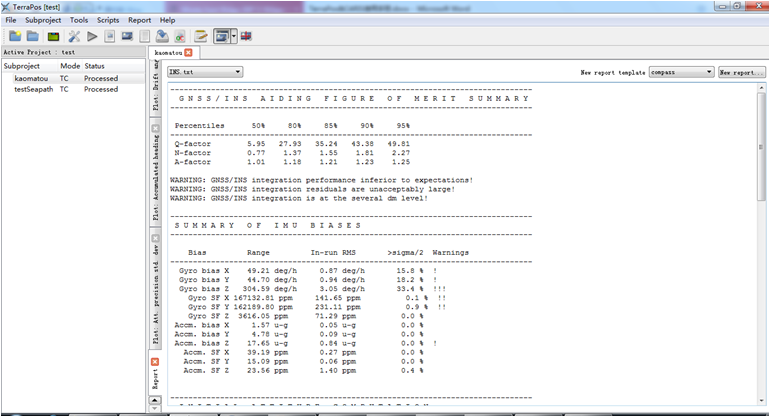
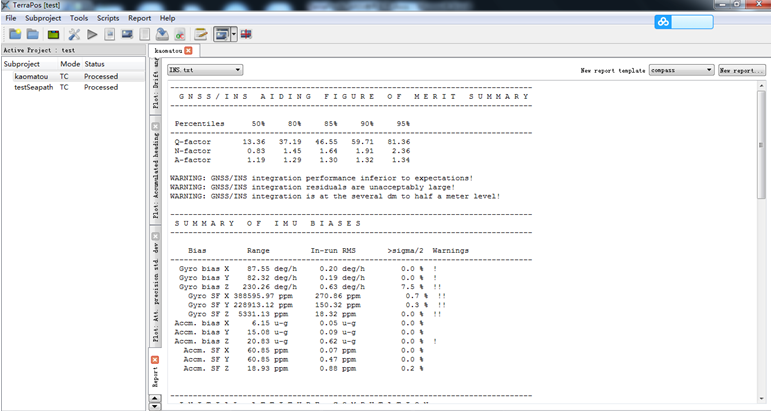
查看INS的精度評定文件,INS.txt
發現羅經誤差較大,出現了報警信號,由于SeaPath采用雙GPS的方式,如果在碼頭,航跡顯示的是一個圓。
上面是采用10s濾波,效果較差,粗差有點多,下面采用1s的濾波
查看精度為overall.txt,發現置信水平為95%是,高程誤差為19.9cm,雖然誤差變化不大,但是高程曲線基本反映了潮位的起伏,但是有一些異常存在,至于這個異常存在,博主認為是卡爾曼濾波有些粗差仍然無法剔除,是不是需要人工剔除才可以?
查看INS的精度評定文件,INS.txt
發現仍然是羅經報警
最后,我搜索了一下關于抗粗差的卡爾曼濾波的論文,有一篇文章魏世玉等《基于卡爾曼濾波的GNSS自動化監測數據粗差分析》
在GNSS( Global Navigation Satellite System) 自動化變形監測中,由于受觀測條件的影響,如周跳、多路徑效應以及接收機信號故障等,致使觀測數據中難免包含粗差,極大降低了觀測成果的準確性和可靠性。粗差的存在給后續變形分析和解釋帶來了困難,甚至得出錯誤結論。因此,粗差探測工作是自動化變形監測數據處理中的重要環節。
對于粗差探測,目前普遍采用以均值漂移模型為基礎的粗差探測和以方差膨脹模型為基礎的抗差估計等 *** 。這些 *** 具備嚴密的理論基礎,當監測網圖形強度較好且具備一定數量的多余觀測時,上述 *** 均能很好地消除粗差對觀測成果的影響。但在GNSS 自動化變形監測中,為了實時掌握變形體變形情況,通常需要提高監測頻率,這就導致一次定位解算的觀測時間變短,多余觀測數也隨之減少。這時按上
述 *** 很難對粗差進行準確的定位和剔除。
卡爾曼濾波是20 世紀60 年代初由卡爾曼等人提出的一種遞推式濾波算法,其更大特點是能夠剔除系統中的隨機干擾,從而獲得逼近真實情況的有用信息。如果將粗差看作GNSS 自動化監測中的隨機干擾,便可利用卡爾曼濾波對其進行剔除,得到一組“干凈”的觀測值序列。因此,本文以GNSS 自動化平面位移監測數據為研究對象,利用卡爾曼濾波,建立監測點坐標序列粗差探測模型,對GNSS 自動化監測坐標序列粗差探測過程進行詳細分析。最后通過實際監測數據分析,驗證該模型的準確性和有效性。
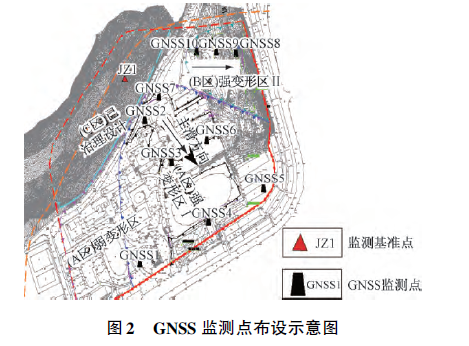
選取同一剖面監測點GNSS2 ( 位于主滑面坡頂)和GNSS4 ( 位于主滑面坡底) 連續1 個月( 2015 年5月) 的監測數據為分析對象,觀測時段長為2 小時( 即連續觀測2 小時的數據作為一次靜態基線解算結果) ,共359 組有效坐標序列數據。
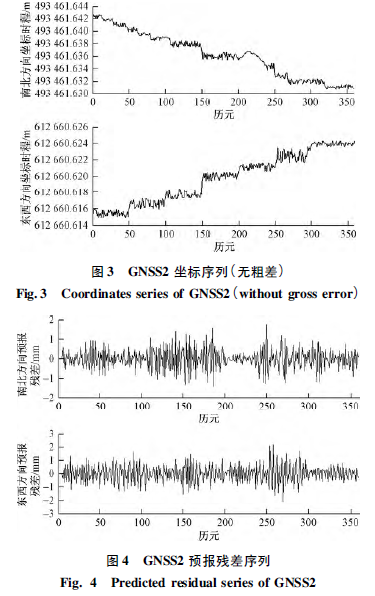
為分析濾波模型對粗差探測的敏感性,選取坡頂觀測條件良好,且距基準站較近的GNSS2 在X 軸和Y軸方向的坐標序列( 圖3) ,經分析發現,該序列無粗差情況。利用前5 個坐標分量序列分別進行二次擬合,以確定初始狀態,從序列第6 個數據開始進行預報與濾波,得其在X 軸和Y 軸方向預報殘差序列見圖4。對上述無粗差坐標序列預報殘差統計分析得X 方向預報殘差中誤差為0. 65 mm,Y 方向則為0. 82 mm。
由此可見,該濾波模型對粗差探測具有較高的靈敏性。
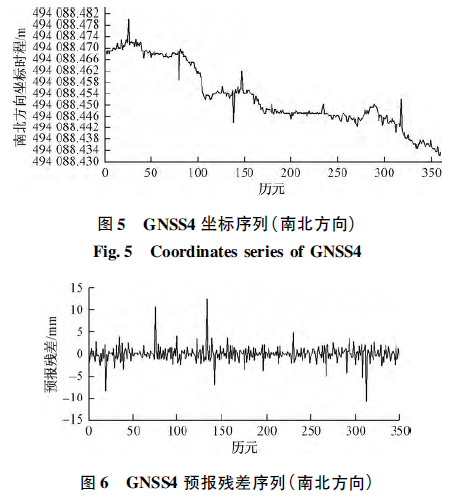
為驗證模型探測粗差的有效性和準確性,選取坡底觀測條件相對較差的GNSS4 在X 軸方向的坐標序列進行分析( 圖5) 。該月監測期間,GNSS4 監測點上接收機存在蓄電池無法供電的情況,導致某些觀測時段觀測值數量不足,另外該監測點位于斜坡底部,衛星信號質量在某些時段可能會較差,因此解算出的坐標序列中極有可能存在粗差。利用前5 個無粗差坐標序列進行二次擬合,以確定濾波初始狀態,并取3 倍擬合殘差中誤差作為粗差探測閾值( μ = 3. 5 mm,μ' = 4. 5mm) ,從序列第6 個數據開始進行預報與濾波,得其在X 軸方向預報殘差序列見圖6。
5 結語
本文將卡爾曼濾波應用于GNSS 自動化監測粗差探測,通過理論分析和實際監測數據驗證,得出以下幾點結論:
( 1) 卡爾曼濾波是一種對動態系統進行實時狀態估計的有效 *** ,系統數學模型和噪聲統計模型的合理建立是系統準確狀態估計的關鍵。
( 2) 實驗分析表明,在啟動卡爾曼濾波之前,較為準確地確定初始狀態及其方差陣D有利于濾波的快速穩定; 動態噪聲和觀測噪聲的不合理選取將導致濾波發散。
( 3) 變形監測數據粗差探測的關鍵在于如何區分粗差與變形。本文利用粗差僅在某一時刻具有突變特征而變形往往伴隨后續數據整體發生偏移,有效地剔除了GNSS 坐標序列中粗差。
是否可以這樣,將GNSS的粗差剔除以后,再重新寫成rinex格式,作為TerraPos的定位數據
原標題:精密單點定位(PPP)數據處理反演潮汐(四) 來源:http://www.xiaokcehui.com/?post=297